作者：Rachel Thomas
翻译：Nothing
审校：loulou
我们所生活的世界似乎是确定的。黑就是黑，白就是白，没有什么含糊不清的东西。一个物体要么在这里要么在那里。但在量子力学里，很多结果因为反直觉而闻名。量子世界中的事物变得模糊不清，确定的事件被概率所代替。一颗粒子可以同时处于不同的位置，我们只能通过波函数计算它在某处的概率是多少。
维纳.海森堡
这种不确定性的背后是量子物理中最著名的原理之一：海森堡不确定性原理（Heisenberg’s uncertainty principle）。1927 年，德国物理学家，维纳 · 海森堡（Werner Heisenberg)，提出了电子位置和动量测量的不确定性原理。这个原理是说从原则上你不可能同时精确的测得电子的位置和动量，你对一个量的测量越准确，对另一个量的测量就越不精确。
如果你把粒子位置的不确定度写为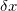 
，将粒子动量的不确定度写为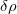 
，那么这两个不确定度之间的关系由下列公式表示：
其中 
是普朗克常量除以 
。
这是表述海森堡不确定性原理最常见的数学形式，两个不确定度的乘积不能小于一个确定值。
令人迷惑的思想实验
海森堡自己想通过以下的思想实验来理解不确定性原理。假设你想确定一个电子的位置，你需要用显微镜观察电子反射的光子。显微镜的精度被光的波长所限制——波长越短显微镜可以达到的精度越高。海森堡提出使用波长非常短的伽马射线来观测电子。
但是相应的，光的波长越短频率就越高，光子携带的能量就越大。海森堡认为你可以通过伽马射线非常精确地测量电子的位置，但是要做到这一点要求至少有一个光子被电子反射。由于伽马射线的光子能量很高，因此碰撞会显著的改变电子的运动状态，也就是影响电子的动量。因此伽马射线显微镜可以很精准地告诉你电子的位置，但是它的扰动使得动量的测量变得不准确。
海森堡的思想实验看似清晰但是却是误导人的，它会让人误以为不确定性是测量对系统的扰动的结果。“海森堡不确定性原理经常被用实验来表述，但是关于它你真正应该思考的是电子本身，”剑桥大学的理论物理学教授 Ben Allanach 说。无论测量与否，该原理涉及到的不确定性是量子世界与生俱来的性质。
对不确定性原理更清楚的认识
尽管海森堡不确定性原理是一个令人感到疑惑的想法，但当你用数学来描述它时，它会变得清晰得多。一个量子系统，例如海森堡考虑的电子。系统在某一时刻的状态由波函数描述，波函数的解只能给出系统具有某种性质的概率。这种概率性导致我们无法准确预测电子的位置。“你考虑的是电子在空间中的分布，”Allanch 说，“如果你测量一个电子，你可以得到测量后它所处的具体位置，但是如果你准备 100 万个处于同一状态的电子然后分别测量它们，你会发现测量到的位置分散在四周。”你所测量到的分散性反映了波函数带来的概率性。你想测量的其他性质也表现出相似的特点，比如动量：你所能预测的只是测得某些动量的概率。
如果你想要从波函数中计算出粒子位置和动量取某些值的概率，需要用到被称为算符的数学工具。量子力学中有很多种算符，例如位置、动量和其他你想了解的性质。这些算符，例如位置算符，作用在波函数上可以得到可能测量到的电子的位置，并且得到测量时电子处于某位置处的概率。每个算符都具有一组被称为本征态的波函数，当电子处于位置本征态描述的状态时，电子处于某个位置的概率是 100%。
对于其他算符来说也是一样的。动量算符同样具有一系列本征态，处于本征态的粒子具有确定的动量。但是从数学上可以看出粒子不可能同时处于动量和位置的本征态。就像 2+3 无论如何也不会等于 27 一样，算符对应的数学要求动量和位置不可能同时处于本征态。（对于熟悉量子力学的人来说，这说明动量和位置算符不可对易。）从数学上讲，想让这样两个力学量同时具有确定值是不可能的。“量子物理的不确定性似乎限制了你对电子的位置和动量测量精度的极限，”Allanach 说，“这是电子本身的性质，不是测量导致的误差。”无论测量与否，你都不可能超越这种不确定性。
量子物理中，同时测量位置和动量的精度存在确定的极限
因为海森堡第一次表述不确定性原理使用的力学量是动量和位置，其他的共轭物理量也存在类似的不确定性原理。这些不确定性导致了量子物理中一系列迷人的结果。如果你仍然觉得这些想法有悖直觉的话，没关系，你不是一个人：爱因斯坦自己对海森堡的不确定性原理和这种现实所带来的“阴云不定”感到震惊。今天的物理学家已经习惯了这些想法，并且正在充分利用这种不确定性。
原文来源：
https://plus.maths.org/content/heisenbergs-uncertainty-principle