
https://en.wikipedia.org/wiki/Rodrigues%27_rotation_formula#Statement
罗德里格斯的旋转公式
这篇文章是关于罗德里格斯的旋转公式,它与相关的欧拉罗德里格斯参数和欧拉罗德里格斯公式的3D旋转不同。
在三维旋转理论中,对于给定旋转轴和旋转角度,以Olinde Rodrigues命名的罗德里格斯公式是用于在空间旋转向量的高效算法。通过扩展,它可以用于把所有轴角表达的三维向量转化为SO(3)中的旋转矩阵,S0(3)是包含所有旋转矩阵的群。换句话说,罗德里格斯公式提供了一种算法来计算从SO(3)的李代数so(3)到李群SO(3)的指数映射,而没有实际计算全矩阵指数。
定义
假设v是R3中的一个向量,并且k是一个描述旋转轴的单位向量,v根据右手规则旋转角度θ,则Rodrigues公式为
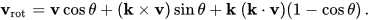
另一种说法是将轴向量作为定义旋转平面的任意两个非零向量a和b的交叉乘积a×b,并且角度θ的方向是从a向b测量的。令α表示这些向量之间的角度,两个角度θ和α不需要等同,但是它们的测量方式相同。 然后可以单位轴向量可以写为
当涉及定义平面的两个向量时,这种形式可能更有用。物理学中的一个例子是托马斯岁差,它包括由罗德里格斯公式给出的旋转,用两个非共线助推速度表示,旋转轴垂直于它们的平面。
求导
令k是定义旋转轴的单位矢量,令v是以角度θ围绕k旋转的任意向量(右手定则,图中逆时针)。
使用点乘和叉乘,向量v可以分解成与轴k平行和垂直的分量,
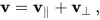
与k平行的分量是
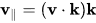
称为v在k上的向量投影,垂直于k的分量为
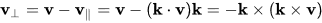
称为k从v的向量拒绝。
矢量k×v可以看作是v⊥逆时针旋转90°左右的副本,所以它们的大小相等,但是方向是垂直的。同样,向量k×(k×v),v⊥的一个副本逆时针旋转180°到k左右,使得k×(k×v)和v⊥的大小相等,但方向相反(即它们是互为负数,因此减号)。扩展矢量三重乘积建立了平行分量和垂直分量之间的连接,参考公式为a×(b×c)=(a·c)b – (a·b)c 给定任意三个向量a,b,c。
平行于轴的分量在旋转下不会改变幅度和方向,
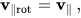
根据以上分析,只有垂直分量才会改变方向,但保持其大小
并且由于k和v||是平行的,所以它们的叉积是零 k×v|| = 0,因此
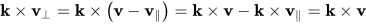
并且
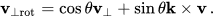
这种旋转是正确的,因为矢量v⊥和k×v具有相同的长度,并且k×v是v⊥围绕k逆时针旋转90°。使用三角函数正弦和余弦对v⊥和k×v进行适当的缩放给出旋转的垂直分量。旋转分量的形式类似于笛卡尔基的2D平面极坐标(r,θ)中的径向向量
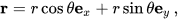
其中ex,ey是它们指示方向上的单位向量。
现在完整的旋转矢量是
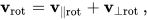
用等式结果中的v ||rot和v⊥rot的定义代替
矩阵表示
将v和k×v表示为列矩阵,叉积可以表示为矩阵乘积
令K表示单位向量k的“叉积矩阵
矩阵方程可以表示为
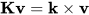
对于任何向量v(实际上,K是具有这个性质的独特矩阵,它具有特征值0和±i)。
迭代右边的交叉乘积相当于乘以左边的交叉乘积矩阵,特别是
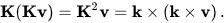
而且,由于k是单位向量,所以K具有单位2-范数。 因此矩阵语言中的上一个旋转公式是
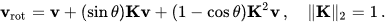
请注意,在这个表示法中,主要术语的系数现在是1。
将v分解可以实现紧凑表达式
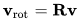
这里
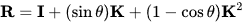
是围绕轴k逆时针旋转角度θ的旋转矩阵,I是3×3单位矩阵。矩阵R是旋转群SO(3)的一个元素,K是李代数的一个元素,所以so(3)生成李群(注意K是负对称的,这表征了so(3)的特性)。 就矩阵指数而言,
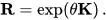
为了理解最后的恒等式,要注意到
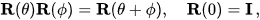
单参数子群的特征,即指数,并且公式与无穷小θ相匹配。
对于基于这种指数关系的替代推导,请参阅从so(3)到SO(3)的指数映射。 对于逆映射,请参见从SO(3)到so(3)的日志映射。




